Advertisements
Advertisements
प्रश्न
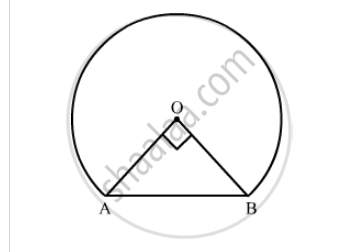
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
उत्तर
We have a cross section of a railway tunnel. `ΔOAB`is a right angled isosceles triangle, right angled at O. let OM be perpendicular to AB.
`OA=2 m`
Use Pythagoras theorem in `ΔOAB`to get,
`AB=(sqrt(2^2+2^2))m`
`= 2sqrt2 m`
Let the height of the tunnel be h. So,
`"Area of" ΔOAB=1/2(2)(2)`
`1/2(2sqrt2)(OM)=2`
Thus,
`OM=sqrt2m`
Therefore,
`h=(2+sqrt2)m`
APPEARS IN
संबंधित प्रश्न
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

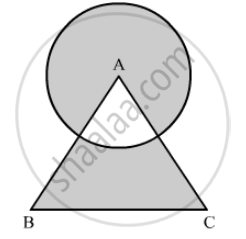
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
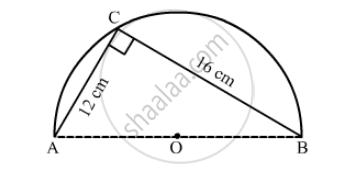
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
