Advertisements
Advertisements
प्रश्न
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
पर्याय
3520 cm2
6400 cm2
7744 cm2
8800 cm2
उत्तर
We have given that a wire is bent in the form of circle of radius 56 cm. If we bent the same wire in the form of square of side a cm, the perimeter of the wire will not change.
∴ perimeter of the circle = perimeter of the square
`∴ 2pi r=4a`
We know that r = 56 cm.
Now we will substitute the value of r in the equation,
`2xxpixx56=4a`............(1)
`∴ 2xx22/7xx56=4a`
`∴2xx22xx8=4a`
Dividing both sides of the equation by 4 we get,
`∴ a=(2xx22xx8)/4`
`∴ a=2xx22xx2`
`∴ a=88`
Now we obtained side of the square. Now we can calculate the area of the square as given below.
Area of the square=`a^2`
Area of the square=`88 ^2`
Area of the square=`7744`
Hence, the area of the square is `7744 cm^2`
APPEARS IN
संबंधित प्रश्न
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
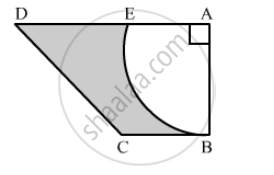
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
If the radius of a circle is doubled, its area becomes ____________.
