Advertisements
Advertisements
प्रश्न
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
उत्तर
Let the radius of the required circle be r.
Now, Area of the required circle = Area of circle having radius 8 cm + Area of circle having radius 6 cm
⇒ πr2 = π(8)2 + π(6)2
⇒ r2 = 64 + 36
⇒ r2 + 102
⇒ r = 10 cm
Hence, the radius of the circle is 10 cm.
APPEARS IN
संबंधित प्रश्न
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
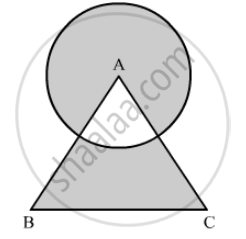
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
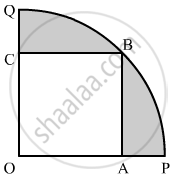
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
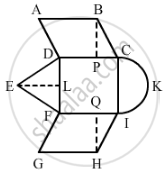
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.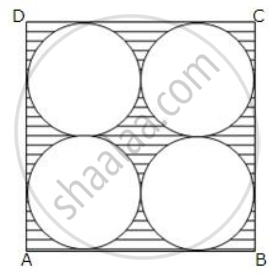
Find the area of the remaining card-board.
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


