Advertisements
Advertisements
प्रश्न
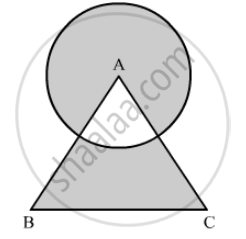
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
उत्तर
In equilateral traingle all the angles are of 60°
∴ ∠BAC = 60°
Area of the shaded region = (Area of triangle ABC − Area of sector having central angle 60°) + Area of sector having central angle (360° − 60°)
\[= \frac{\sqrt{3}}{4} \left( AB \right)^2 - \frac{60°}{360°}\pi \left( 7 \right)^2 + \frac{300°}{360°}\pi \left( 7 \right)^2 \]
\[ = \frac{\sqrt{3}}{4} \left( 14 \right)^2 - \frac{1}{6} \times \frac{22}{7} \left( 7 \right)^2 + \frac{5}{6} \times \frac{22}{7} \left( 7 \right)^2 \]
\[ = 84 . 77 - 25 . 67 + 128 . 35\]
\[ = 187 . 45 {cm}^2\]
Hence, the area of shaded region is 187.45 cm2
APPEARS IN
संबंधित प्रश्न
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is ______.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
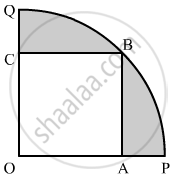
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
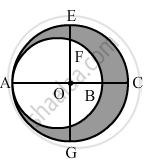
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
