Advertisements
Advertisements
प्रश्न
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
उत्तर
Let the radius of the circle be r and side of hexagon be a.
Area of hexagon =\[\frac{3\sqrt{3}}{2} a^2\]
\[\Rightarrow 24\sqrt{3} = \frac{3\sqrt{3}}{2} a^2 \]
\[ \Rightarrow a^2 = 16\]
\[ \Rightarrow a = 4 cm\]
In an regular hexagon inscribed in a circle, its side is equal the radius.
∴ r = a = 4 cm
Now, Area of circle is given by
\[\pi r^2 \]
\[ = 3 . 14 \times 4 \times 4\]
\[ = 50 . 24 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
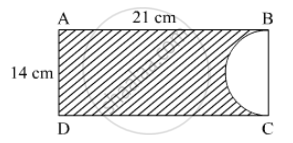
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
The floor of a rectangular hall is 24 m long and 18 m wide. How many carpets, each of length 2.5 m and breadth 80 cm, will be required to cover the floor of the hall?
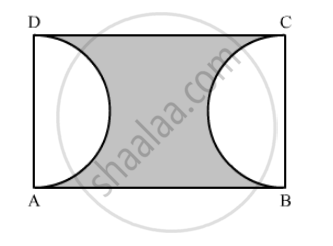
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

Write the area of the sector of a circle whose radius is r and length of the arc is l.
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
