Advertisements
Advertisements
प्रश्न
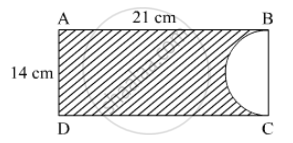
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
उत्तर
Area of the shaded region = Area of the rectangle − Area of the semicircle
`= 21 xx 14 - {1/2xx pi xx(14/2)^2}`
`=294 - {1/2 xx 22/7 xx 7 xx 7}`
= 297- 77
`= 217 cm^2`
Therefore area of shaded region is `217 cm^2`
= AB + AD + DC + BC
`= AB + AD + DC + 1/2 xx 2pi (14/2)`
`= 21 + 14 + 21 + 22/7 xx 7`
= 56 + 22
= 78 cm
Therefore the perimeter of the shaded region is 78 cm
APPEARS IN
संबंधित प्रश्न
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

The area of the largest triangle that can be inscribed in a semi-circle of radius r is
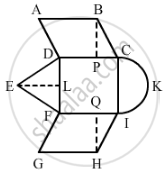
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The area of the sector of angle θ° of a circle with radius R is
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
A lawn is in the shape of a semicircle of diameter 42m. the lawn is surrounded by a flower bed of width 7m all round. Find the area of the flower bed in m2.
