Advertisements
Advertisements
प्रश्न
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
उत्तर
Since the diameter of the circle is the diagonal of the square inscribed in the circle.
Let a be the length of the sides of the square.
Hence,
`sqrt2a` = 2 x 7
a = `sqrt2` x 7
a2 = 98
Hence the area of the square is 98 sq.cm.
APPEARS IN
संबंधित प्रश्न
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
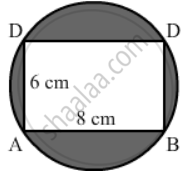
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


