Advertisements
Advertisements
प्रश्न
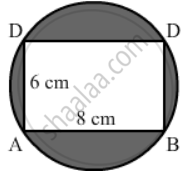
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
पर्याय
264 cm2
266 cm2
272 cm2
254 cm2
None of the above.
उत्तर
None of the above
Explanation:
All options are incorrect; the correct answer is 30.5 cm.
Join AC.
Now, AC is the diameter of the circle.
We have:
AC2 = AB2 + BC2 [By pythagoras' theorem]
⇒ AC2 = {(8)2 + (6)2} cm2
⇒ AC2 = (64 + 36) cm2
⇒ AC2 = 100 cm2
∴ Radius of the circle`=10/2 "cm"`
= 5 cm
Now,
Area of the shaded region = Area of the circle with radius 5 cm − Area of the rectangle ABCD
`=|(3.14xx5xx5)-(8xx6)| "cm"^2`
`=|(314/100xx25)-48| "cm"^2`
`=(157/2-48) "cm" ^2`
`=61/2 "cm" ^2`
= 30.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 600 .
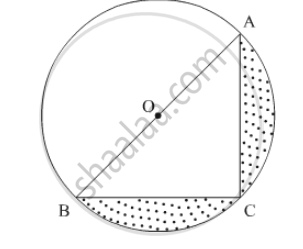
Find the area of the shaded region in the following figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)
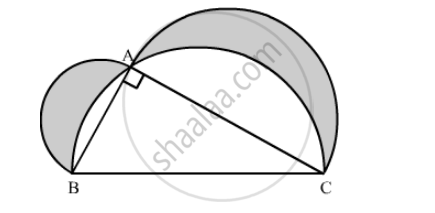
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

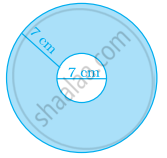
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
Find the area of the shaded region: