Advertisements
Advertisements
प्रश्न
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
उत्तर
Side of the equilateral triangle = 12 m
Area of the equilateral triangle `= sqrt(3)/4xx("Side")^2`
`=sqrt(3)/4xx12xx12`
Length of the rope = 7 m
Area of the field the horse can graze is the area of the sector of radius 7 m .Also, the angle subtended at the centre is 60°
`=theta/360xxpi"r"^2`
`=60/360xx22/7xx(7)^2`
= 25.67 m2
Area of the field the horse cannot graze = Area of the equilateral triangle -- Area of the field the horse can graze
= 62.28 - 25.67 = 36.61 m2
APPEARS IN
संबंधित प्रश्न
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is `3375m^2` . Find the cost of fencing the lawn at ₹ 65 per metre.
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
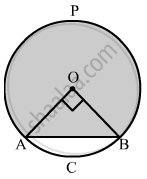
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
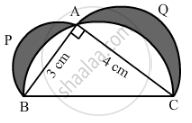
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
Area of a quadrant of a circle of radius 7 cm is ______.
