Advertisements
Advertisements
प्रश्न
A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is `3375m^2` . Find the cost of fencing the lawn at ₹ 65 per metre.
उत्तर
Let the length and breadth of the rectangular lawn be 5xmand3 xm, respectively.
Given:
Area of the rectangular lawn `3375m^2`
⇒`3375=5x xx 3x`
⇒`3375=15x^2`
⇒`3375/15=x^2`
⇒`225=x^2`
⇒ `x=15`
Thus, we have:
`l=5x=5xx15=75m`
`b=3x=3xx15=45 m`
Perimeter of the rectangular lawn =`2(l+b) `
=`2(75+45) `
=`2(120) `
=`240 m`
Cost of fencing 1 m lawn = Rs 65
∴ Cost of fencing 240 m lawn = `240xx65=Rs 15,600`
APPEARS IN
संबंधित प्रश्न
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
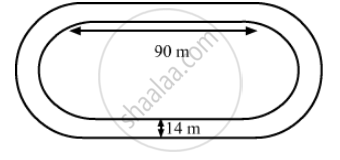
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
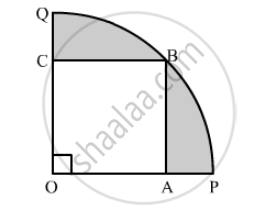
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
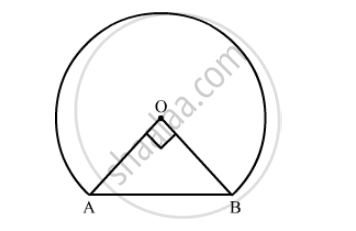
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If diameter of a circle is increased by 40%, then its area increase by
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
A 7m wide road surrounds a circular garden whose area is 5544m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per m2.
