Advertisements
Advertisements
प्रश्न
If diameter of a circle is increased by 40%, then its area increase by
पर्याय
96%
40%
80%
48%
उत्तर
If d is the original diameter of the circle, then the original radius is `d/2`
∴ area of the circle =`pi (d/2)^2`
∴ area of the circle=`pixxd^2/4`
If diameter of the circle increases by 40%, then new diameter of the circle is calculated as shown below,
That is new diameter=`d+04 d`
`=1.4 d`
∴ new radius=`(1.4 d)/2`
∴ new radius=`0.7 d`
So, new area will be` pi(0.7 d)^2`
∴ New radius=`pixx0.49 d^2`
Now we will calculate the change in area.
∴ Change in area =`pixx0.49d^2-pixxd^2/4`
∴ change in area=`(0.49-1/4)pid^2`
∴ change in area=`0.96 pi d^2/4`
Therefore, its area is increased by `96%`
APPEARS IN
संबंधित प्रश्न
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
If the difference between the circumference and radius of a circle is 37 cm, then its area is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
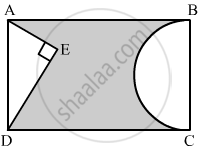
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
A sprinkler placed at the centre of a flower garden sprays water covering a circular area. If the area watered is 1386 cm2, find its radius and diameter
