Advertisements
Advertisements
Question
If diameter of a circle is increased by 40%, then its area increase by
Options
96%
40%
80%
48%
Solution
If d is the original diameter of the circle, then the original radius is `d/2`
∴ area of the circle =`pi (d/2)^2`
∴ area of the circle=`pixxd^2/4`
If diameter of the circle increases by 40%, then new diameter of the circle is calculated as shown below,
That is new diameter=`d+04 d`
`=1.4 d`
∴ new radius=`(1.4 d)/2`
∴ new radius=`0.7 d`
So, new area will be` pi(0.7 d)^2`
∴ New radius=`pixx0.49 d^2`
Now we will calculate the change in area.
∴ Change in area =`pixx0.49d^2-pixxd^2/4`
∴ change in area=`(0.49-1/4)pid^2`
∴ change in area=`0.96 pi d^2/4`
Therefore, its area is increased by `96%`
APPEARS IN
RELATED QUESTIONS
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
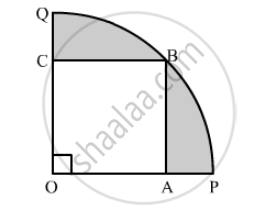
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
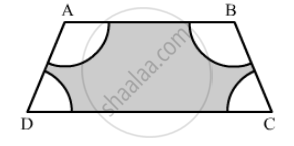
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
In the following figure, the shaded area is

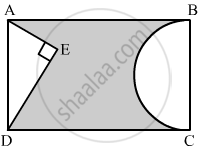
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
Find the area of the dining table whose diameter is 105 cm
