Advertisements
Advertisements
Question
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
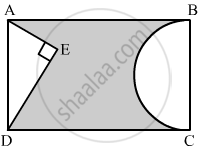
Solution
We know that the opposite sides of a rectangle are equal
AD = BC = 70 cm
In right triangle AED
AE2 = AD2 − DE2
= (70)2 − (42)2
= 4900 − 1764
= 3136
∴ AE2 = 3136
⇒ AE = 56
= Area of the shaded region = Area of rectangle − (Area of triangle AED + Area of semicircle)
`= "AB"xx"BC"-[1/2xx"AE"xx"DE" + 1/2pi("BC"/2)^2]`
`= 80xx70-[1/2xx56xx42+1/2xx22/7(70/2)^2]`
= 5600 - 3101
= 2499 cm2
Hence, the area of shaded region is 2499 cm2
APPEARS IN
RELATED QUESTIONS
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
If diameter of a circle is increased by 40%, then its area increase by
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
