Advertisements
Advertisements
Question
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
Solution
We know area of minor segment of the circle is \[A = \left\{ \frac{\pi\theta}{360} - \sin\frac{\theta}{2}\cos\frac{\theta}{2} \right\} r^2\]
\[\Rightarrow A = \left\{ \frac{\pi \times 90°}{360} - \sin\frac{90}{2}\cos\frac{90}{2} \right\} \left( 20 \right)^2 \]
\[ \Rightarrow A = \left( \frac{\pi}{4} - \frac{1}{2} \right)\left( 400 \right)\]
Area of the major segment = Area of the circle − area of the minor segment
\[= \pi \left( 20 \right)^2 - \left( 400 \right)\left[ \frac{\pi}{2} - \frac{1}{2} \right]\]
\[ = \left( 400 \right)\left[ \pi - \frac{\pi}{2} + \frac{1}{2} \right]\]
\[ = 1142 {cm}^2\]
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

The area of a circle is 220 cm2. The area of ta square inscribed in it is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
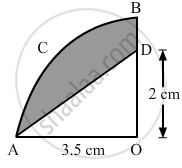
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
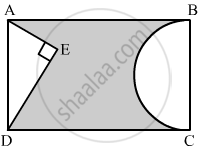
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
