Advertisements
Advertisements
Question
Find the area of minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 600 .
Solution
Area of the minor segment of the circle = \[\sqrt{2}\]\[\frac{\theta}{360} \times \pi r^2 - r^2 \sin\frac{\theta}{2}\cos\frac{\theta}{2}\]
\[= \frac{60}{360} \times \pi \left( 14 \right)^2 - \left( 14 \right)^2 \sin\frac{60}{2}\cos\frac{60}{2}\]
\[ = \left( 14 \right)^2 \left[ \frac{1}{6}\pi - \frac{1}{2} \times \frac{\sqrt{3}}{2} \right]\]
\[ = \left( \frac{308}{3} - 49\sqrt{3} \right) {cm}^2\]
APPEARS IN
RELATED QUESTIONS
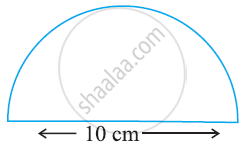
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
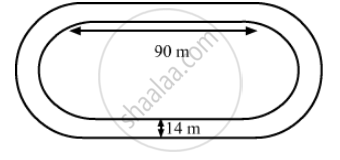
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
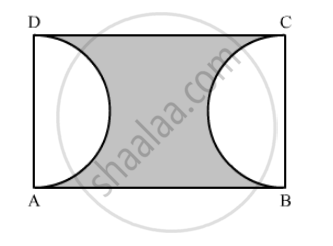
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
The area of a circle is 220 cm2. The area of ta square inscribed in it is
If the radius of a circle is diminished by 10%, then its area is diminished by
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
