Question

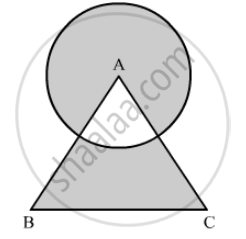
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to

Options

• \[\left( \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) r^2\]

• \[\left( \frac{\pi}{3} - \frac{\sqrt{3}}{2} \right) r^2\]

• \[\left( \frac{\pi}{3} + \frac{\sqrt{3}}{4} \right) r^2\] 

• \[\left( \frac{\pi}{3} + \sqrt{3} \right) r^2\]

Answer 1

We have given that ABC is an equilateral triangle.

`∴ ∠A=60°`

As we know that,`∠BCA=1/2 m (∠BOC)`

`∴ 60=1/2 m (BOC)`

`m(∠BOC)=120°`

Area of the shaded region = area of the segment BC.

Let  `∠BOC=θ`

∴ Area of the segment= `(piθ/360-sin  θ/2 cos  θ/2)`

Substituting the values we get,

Area of the segment= `((pixx120)/360-sin60cos60)r^2`

∴ Area of the segment=`(pi/3-sin60cos60)r^2`

Substituting `sin 60=sqrt3/2` and `60=1/2`we get, 

∴ Area of the segment=`(pi/3-1/2xxsqrt3/2)r^2`

∴ Area of the segment=`(pi/3-sqrt3/4)r^2`

Therefore, area of the shaded region is` (pi/3-sqrt3/4)r^2`.