Advertisements
Advertisements
Question
The area of a circular path of uniform width h surrounding a circular region of radius r is
Options
\[\pi(2r + h)r\]
\[\pi(2r + h)r\]
\[\pi(2r + h)h\]
\[\pi(h + r)r\]
\[\pi(h + r)h\]
Solution

We have
`OA=r`
`AB=h`
Therefore, radius of the outer circle will be.`r+h`
Now we will find the area between the two circles.
∴Area of the circular path=`pi(r+h)^2-pir^2`
∴Area of the circular path=`pi(r^2+2rh+h^2)-pir^2`
∴Area of the circular path=`pi(r^2+2rh+h^2-r^2)`
Cancelling `r^2 "we get"`
∴Area of the circular path=`pi(2rh+h^2)`
∴Area of the circular path=`pi(2r+h)h`
Therefore,are of the circle is `pi(2r+h)h`
APPEARS IN
RELATED QUESTIONS
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
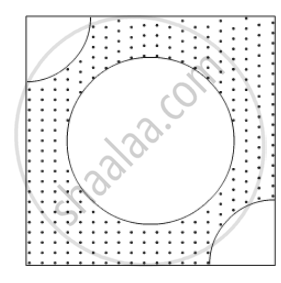
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
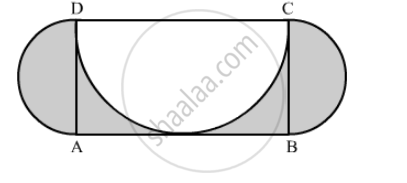
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
If the area of the circle is numerically equal to twice its circumference then what is the diameter of the circle?
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
The area of the circle whose diameter is 21 cm is ____________.
Find the area of the shaded region:
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
