Advertisements
Advertisements
Question
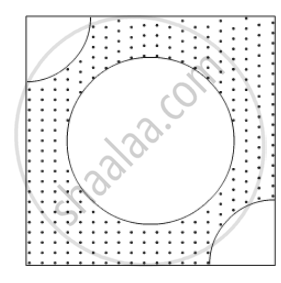
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
Solution
It is given that a circle of radius 4.2 cm and two quadrants of radius 1.4 cm are cut from a square of side 8 cm.
Let the side of square be a. Then,
Area of squre=`a^2`
`=8xx8`
`=64 cm^2`
\[Area of circle = \pi r^2 \]
\[ = \frac{22}{7} \times 4 . 2 \times 4 . 2\]
\[ = 55 . 44 {cm}^2\]
Now area of quadrant of circle of radius 1.4 cm is,
Area of quadrant =`1/4pir^2`
` =1/4xx22/7xx1.4xx1.4`
`=1.54 cm^2`
\[Area of circle = \pi r^2 \]
\[ = \frac{22}{7} \times 4 . 2 \times 4 . 2\]
\[ = 55 . 44 {cm}^2\]
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
What is the area of a square inscribed in a circle of diameter p cm ?
The perimeter of the sector OAB shown in the following figure, is

If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
Area of a circle with diameter ‘m’ radius ‘n’ and circumference ‘p’ is ______.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
