Advertisements
Advertisements
Question
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
Solution
Area of the circle = sum of areas of 2 circles
πR2 = π(40)2 + π(9)2
πR2 = π × (402 + 9)2
R2 = 1600 + 81
R2 = 1681
R = 41 cm.
Diameter of required circle = 41 × 2 = 82 cm
APPEARS IN
RELATED QUESTIONS
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
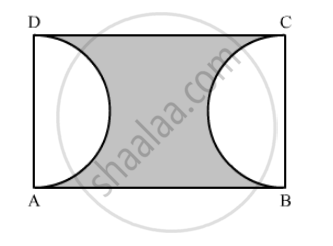
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
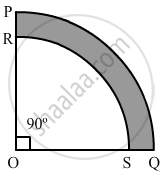
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
On increasing the diameter of a circle by 40%, its area will be increased by
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
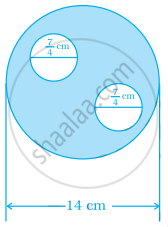
On a square cardboard sheet of area 784 cm2, four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
Find the area of the shaded region: