Advertisements
Advertisements
Question
On a square cardboard sheet of area 784 cm2, four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
Solution
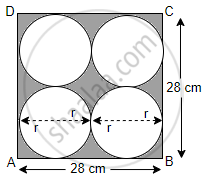
Let a be the side of square ABCD.
Area of square ABCD = 784 cm2
⇒ a2 = 784
⇒ a = `sqrt(784)`
= `sqrt(2 xx 2 xx 2 xx 2 xx 7 xx 7)`
= 2 × 2 × 7
⇒ a = 28 cm
Now, in four circles,
4r = AB
⇒ 4r = 28 cm
⇒ r = 7 cm
Area enclosed between circles and square
= Area of square – Area of 4 circles
= 784 – 4πr2
= `784 - 4 xx 22/7 xx 7 xx 7`
= 784 – 616
= 168 cm2
Hence, the area of square sheet not covered by circular plates is 168 cm2.
APPEARS IN
RELATED QUESTIONS
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
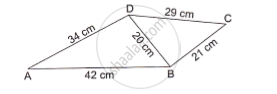
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
