Advertisements
Advertisements
Question
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
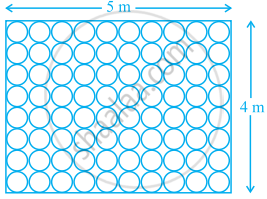
Solution
Given, floor of a room is covered with circular tiles.
Length of a floor of a room (l) = 5 m
And breadth of floor of a room (b) = 4 m
∴ Area of floor of a room = l × b
= 5 × 4
= 20 m2
⇒ Radius of each circular tile (r) =
= 25 m
=
=
Now, area of a circular tile = πr2
=
=
∴ Number of circular tiles = 80
∴ Area of 80 circular tiles
=
= 5 × 3.14
= 15.7 m2
So, area of floor that remains uncovered with tiles = Area of floor of a room – Area of 80 circular tiles
= 20 – 15.7
= 4.3 m2
Hence, the required area of floor that remains uncovered with tiles is 4.3 m2.
APPEARS IN
RELATED QUESTIONS
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
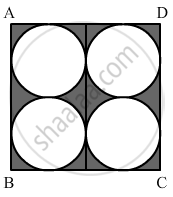
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
