Question

All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm². (Use π = 3.14)

Answer 1

Given that the area of the circle is 1256 cm².

πr² = 12563.14 × r²

3.14 × r² = 1256

r² = `1256/3.14`

r² = 400

r = 20 cm

If all the vertices of a rhombus lie on a circle, then the rhombus is square.

Consider the following figure.

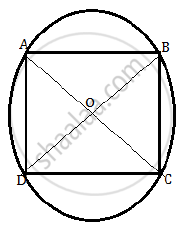
Here A, B, C and D are four points on the circle.

Thus, OA = OB = OC = OD = radius of the circle.

⇒ AC and BD are the diameters of the circle.

Consider the ΔADC.

By Pythagoras theorem, we have,

AD² + CD² = AC²

2AD² = (2 × 20)²  ...[AD = CD]

2AD² = (40)²

AD² = `1600/2`

AD² = 800 cm²

If AD is the side of the square, then AD² is the area of the square.

Thus area of the square is 800 cm².