Advertisements
Advertisements
Question
The diameter of a cycle wheel is `4 5/11` cm. How many revolution will it make in moving 6.3 km ?
Solution
Diameter = `4 5/11` cm = `49/11` cm
circumference = 2 π r = π d
`= 22/7 xx 49/11`
= 14 cm
Circumference= 14 cm = 0.14m
Distance travelled = 6.3 km = 6300 m
No. of revolutions = `6300/0.14 = 45000`
Wheel takes 45000 revolutions in moving 6.3 km
APPEARS IN
RELATED QUESTIONS
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. (Use π = 3.14)
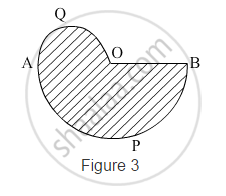
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
A bicycle whell makes 5000 revolutions in moving 11 km. Find the diameter of the wheel
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)

Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
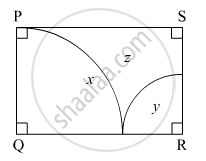
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
The circumferences of two circles are in the ratio 3 : 4. The ratio of their areas is
The radius of the circle is given below; find the area.
28 cm
Find the circumference of the circle whose area is 25 times the area of the circle with radius 7 cm.
The speed of the car is 66 km/hour. If each wheel of the car is 140 cm in diameter, find the number of revolutions made by each wheel per minute.
The diameter of a right circular cylinder is 12 m and the slant height is 10 m. Find its curved surface area and the total surface area .
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
Draw the circumcircle of Δ PMT in which PM = 5.4, P = 60°, M = 70°.
The radius of two circles are 20 cm and 13 cm. Find the difference between their circumferences. (Take π =`22/7`)
The center O of a circle of a radius 1.3 cm is at a distance of 3.8 cm from a given straight line AB. Draw a circle to touch the given straight line AB at a point P so that OP = 4.7 cm and to touch the given circle externally.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | ...... | 616 cm |
