Advertisements
Advertisements
Question
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
Solution
Distance = 4.95 km = 4.95 × 1000 × 100 cm
∴ Distance covered by the wheel in 1 revolution `= "Total distance covered"/"Number of revolutions"`
`=(4.95xx1000xx100)/2500`
= 198 cm
Now,
Circumference of the wheel = 198 cm
⇒ 2πr = 198
`⇒ 2 ×22/7xx"r" = 198`
`=> "r" =(198xx7)/44`
⇒ r = 31.5 cm
∴ Diameter of the wheel = 2r
= 2(31.5)
= 63 cm
APPEARS IN
RELATED QUESTIONS
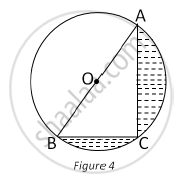
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
Choose the correct alternative answer for the following question.
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is `32sqrt(3)`, find the radius of the circle.
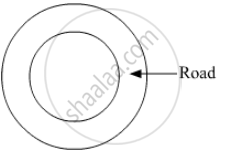
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket. (Take π =22/7)
Find the area and perimeter of the following semicircles: Radius = 1.4cm
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
Is it true that the distance travelled by a circular wheel of diameter d cm in one revolution is 2 π d cm? Why?
A dinner plate is in the form of circle. A circular region encloses a beautiful design as shown in the given figure. The inner circumference is 352 mm and outer is 396 mm. Find the width of circular design.

