Advertisements
Advertisements
Question
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
Solution

Let the three regions be A, B and C.
The diameters are in the ratio 1 : 2 : 3.
Let the diameters be 1x, 2x and 3x
Then the radius will be `x/2, (2x)/2` and `(3x)/2`
Area of region A = `pi"r"_"A"^2`
= `pi(x/2)^2`
= `pix^2/4`
Area of region B = `pi"r" _"B"^2-pi"r" _"A"^2`
= `pi(x)^2-pi(x/2)^2`
= `(3pi(x)^2)/4`
Area of region C = `pi"r"_"C"^2-pi"r"_"B"^2-pi"r"_"A"^2`
= `pi((3x)/2)^2-pi(x)^2-pi(x/2)^2`
= `pi((3x)/2)^2-(3pix^2)/4`
= `(5pix^2)/4`
Thus, ratio of the areas of regions A, B and C will be
`pix^2/4 : (3pi(x)^2)/4 : (5pix^2)/4`
⇒ 1 : 3 : 5
APPEARS IN
RELATED QUESTIONS
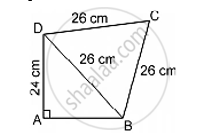
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
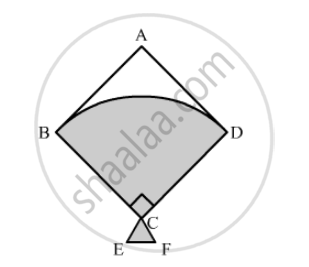
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
The area of a circle is 98.56 cm2. Find its circumference.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
A lawn is in the shape of a semicircle of diameter 42m. the lawn is surrounded by a flower bed of width 7m all round. Find the area of the flower bed in m2.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
