Advertisements
Advertisements
Question
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
Solution
Dimension of the rectangular card board = 14 cm × 7 cm
Since, two circular pieces of equal radii and maximum area touching each other are cut from the rectangular card board, therefore, the diameter of each of each circular piece is 14/2 = 7 cm.
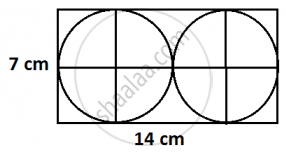
Radius of each circular piece = `7/2`cm
∴ Sum of area of two circular pieces==`2xxpi(7/2)^2=2xx22/7xx49/7=77 cm^2`
Area of the remaining card board = Area of the card board − Area of two circular pieces
= 14 cm × 7 cm − 77 cm2 = 98 cm2 − 77 cm2 = 21 cm2
Thus, the area of the remaining card board is 21 cm2.
APPEARS IN
RELATED QUESTIONS
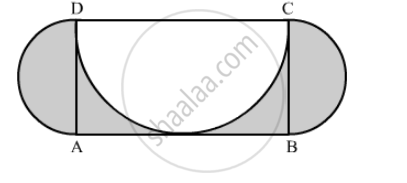
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
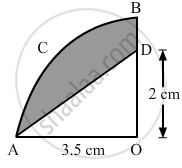
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

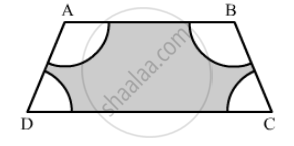
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The cost of fencing a circular field at the rate of Rs 25 per metre is Rs 5500. The field is to be ploughed at the rate of 50 paise per m2 . Find the cost of ploughing the field. [Take `π =22/7`].
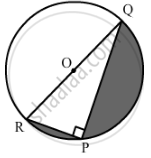
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
On decreasing the radius of a circle by 30%, its area is decreased by
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
