Advertisements
Advertisements
Question
On decreasing the radius of a circle by 30%, its area is decreased by
Options
30%
60%
45%
none of these
Solution
None of these
Let r be the original radius.
Thus, we have:
Original area = πr2
Also,
New radius = 70% of r
`=(70/100xx""r")`
`= (7"r")/10`
New area `= pixx((7"r")/10)^2`
`= (49pi"r"^2)/100`
Decrease oin the area`=(pi"r"^2 = (49pi"r"^2)/100)`
`=(59pi"r"^2)/100`
Thus, we have;
Decrease in the area`=((59pi"r"^2)/100xx1/pi"r"^2xx100)%`
= 51%
APPEARS IN
RELATED QUESTIONS
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
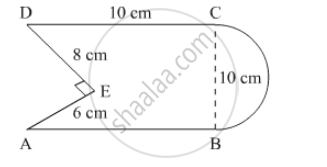
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
The area of the circle that can be inscribed in a square of side 10 cm is
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
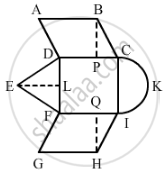
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
A 7m wide road surrounds a circular garden whose area is 5544m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per m2.
Area of circle of radius ‘n’ units is
