Advertisements
Advertisements
Question
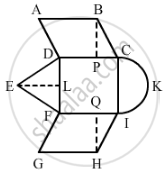
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
Solution
CD = 8 cm
BP = HQ = 4 cm
DE = EF = 5 cm
Area of the parallelogram ABCD `="B"xx"H"`
= 8 × 4
= 32 sq. cm
Area of parallelogram ABCD = B × H
= 8 × 4
= 32 sq.cm
Area of parallelogram FGHI = B × H
= 8 × 4
= 32 sq. cm
Area of the square = Side2
= 82 = 64 sq.cm
In Δ ELF, we have:
EL2 = 52 - 42
EL2 = 9
EL = 3 cm
Area of ΔDEF `=1/2xx"B"xx"H"`
`= 1/2xx8xx3`
= 12 sq.cm
Area of the semicircle = `1/2pi"r"^2`
`=1/2xx22/7xx16`
= 25.12 sq.cm
∴ Total Area = Area of the parallelogram ABCD + Area of the parallelogram FGHI + Area of the triangle DEF + Area of the semicircle CKI + Area of the square
Total Area = 165.12 cm2
APPEARS IN
RELATED QUESTIONS
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The length of an arc of the sector of angle θ° of a circle with radius R is
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.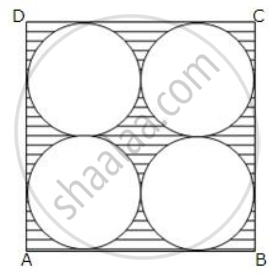
Find the area of the remaining card-board.
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
