Advertisements
Advertisements
Question
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
Solution
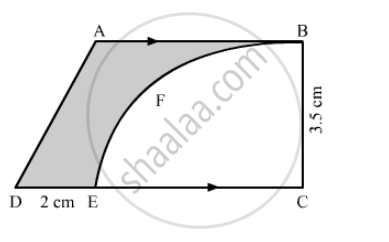
We have given a trapezium. We are asked to find the area of the shaded region.
We can find the area of the remaining part that is area of the shaded region as shown below.
`"Area of the shaded region = Area of the trapezium-Area of the sctor"`
`∴ "Area of the shaded region"=1/2 (AB+CD)xxBC-θ/360 pir^2`
`∴ "Area of the shaded region"=1/2(3.5+CD)xx3.5-90/360 pi(3.5)^2 .............(1)`
Now we find the value of CD.
`CD=CE+DE`
`∴ CD=3.5+2` ..................(Since, CE is radius of the sector, therefore, CE = 3.5)
`∴ CD=5.5`
Substituting the values of CD and `pi=22/7`in equation (1),
`∴ "Area of the shaded region" = 1/2(3.5+5.5)xx3.5-90/360xx22/7xx(3.5)^2`
`∴ "Area of the shaded region"=31.5/2-1/4xx22xx0.5xx3.5`
`∴ "Area of the shaded region"=31.5/2-1/2xx11xx0.5xx3.5`
`∴ "Area of the shaded region"=31.5/2-19.25/2`
`∴ "Area of the shaded region"=12.25/2`
`∴ "Area of the shaded region"=6.125`
Therefore, area of the remaining part is `6.125 cm^2`
APPEARS IN
RELATED QUESTIONS
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
Area of the circle obtained in 196 m2 is ______.
