Question

From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.

Answer 1

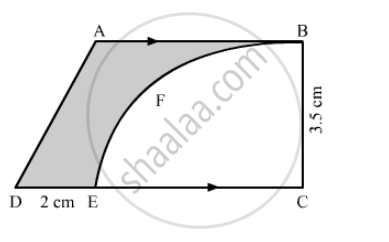
We have given a trapezium. We are asked to find the area of the shaded region.

We can find the area of the remaining part that is area of the shaded region as shown below.

`"Area of the shaded region = Area of the trapezium-Area of the sctor"` 

`∴ "Area of the shaded region"=1/2 (AB+CD)xxBC-θ/360 pir^2`

`∴ "Area of the shaded region"=1/2(3.5+CD)xx3.5-90/360 pi(3.5)^2 .............(1)` 

Now we find the value of CD. 

`CD=CE+DE` 

`∴ CD=3.5+2` ..................(Since, CE is radius of the sector, therefore, CE = 3.5)

`∴ CD=5.5`

Substituting the values of CD and `pi=22/7`in equation (1), 

`∴ "Area of the shaded region" = 1/2(3.5+5.5)xx3.5-90/360xx22/7xx(3.5)^2`

`∴ "Area of the shaded region"=31.5/2-1/4xx22xx0.5xx3.5`

`∴ "Area of the shaded region"=31.5/2-1/2xx11xx0.5xx3.5`

`∴ "Area of the shaded region"=31.5/2-19.25/2`

`∴ "Area of the shaded region"=12.25/2`

`∴ "Area of the shaded region"=6.125`

Therefore, area of the remaining part is `6.125 cm^2`