Advertisements
Advertisements
Question
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
Solution

In this figure, centre of the circle is O, radius OA = r and ∠ AOB=θ
We are going to find the area of the segment AXB.
Area of the segment AXB=Area of the sector `OAXB-"Area of" ΔAOB`...........(1)
We know that area of the sector `OAXB=θ/360xxpi r^2`
We also know that area of `ΔAOB=r^2 sin θ/2 cos θ/2`
Substituting these values in equation (1) we get,
`"Area of the segment AXB"=θ/360 xxpi r^2-r^2 sin θ/2 cos θ/2`
`"Area of the segment AXB"=(θ/360 xxpi-sin θ/2 cos θ/2 )r^2`
`"So Area of the segment AXB"=((piθ)/360-sin θ/2 cos θ/2 )r^2`
Therefore, area of the segment is` ((piθ)/360-sin θ/2 cos θ/2) r^2`
APPEARS IN
RELATED QUESTIONS
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
In the following figure, the shaded area is

Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
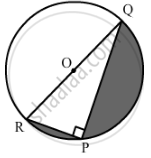
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
