Advertisements
Advertisements
Question
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
Solution
Let the radius of outer circle = R cm
And, the radius of inner circle = r cm
Then, we have
R - r = 1 ....(i)
And, π(R2 - r2) = 88
⇒ (R - r)(R + r)
= `88 xx (7)/(22)`
⇒ 1 x (R + r) = 28
⇒ R + r = 28 ....(ii)
Adding (i) and (ii), we get
2R = 29
⇒ R = 14.5cm
Now, R + r = 28
⇒ 14.5 + r = 28
⇒ r = 13.5cm.
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that diameter = 49 m.
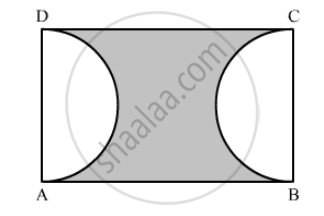
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
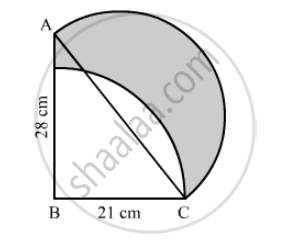
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
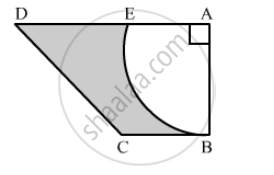
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
If the difference between the circumference and radius of a circle is 37 cm, then its area is
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
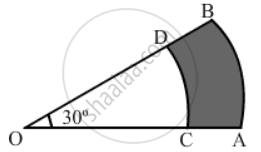
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
