Advertisements
Advertisements
Question
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
Options
17 \[\sqrt{3}\]units
36 units
72 units
48\[\sqrt{3}\]units
Solution
Let the circle of radius r be inscribed in an equilateral triangle of side a.
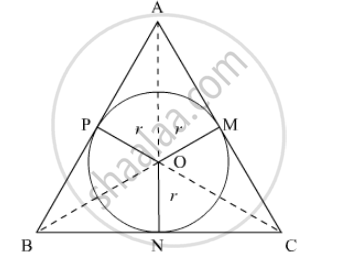
Area of the circle is given as 48π.
`⇒ pir^2=48pi`
`⇒ r^2=48`
`⇒ r=4sqrt3`
Now, it is clear that ON⊥BC. So, ON is the height of ΔOBC corresponding to BC.
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB = 3 × Area of ΔOBC
`sqrt3/4xxa^2=3xx1/2xxBCxxON`
`sqrt3/4xxa^2=3xx1/2xxaxxr`
`sqrt3/4xxa^2=3xx1/2xxaxx4sqrt3`
`a=24`
Thus, perimeter of the equilateral triangle = 3 × 24 units = 72 units
APPEARS IN
RELATED QUESTIONS
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
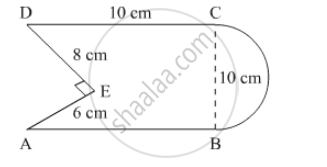
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

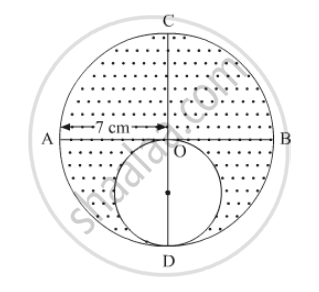
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
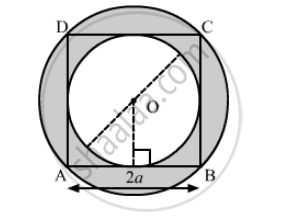
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
The area of the incircle of an equilateral triangle of side 42 cm is
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
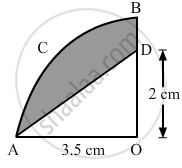
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
