Advertisements
Advertisements
Question
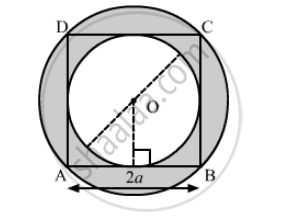
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
Solution
We have a square ABCD having`AB=2c`. From the given diagram we can observe that,
Radius of incircle `(r_1)=a`
Radius of circumcircle `(r_2)=sqrt2a`
(i) We have to find the ratio of the circumferences of the two circles. So the required ratio is,
=` "Perimeter of inner circle "/"Perimeter of circumcircle" `
`=(2pi(a))/(2 pi(sqrt2a))`
`= 1/sqrt2`
(ii) We have to find the ratio of the areas of the two circles. So the required ratio is,
`= "Area of inner circle"/"Area of circumcircle"`
`= (pi(a)^2)/(pi(sqrt2a)^2)`
`=1/2`
APPEARS IN
RELATED QUESTIONS
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
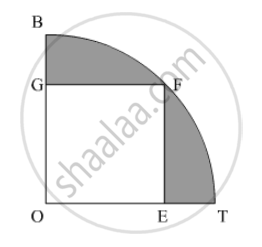
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
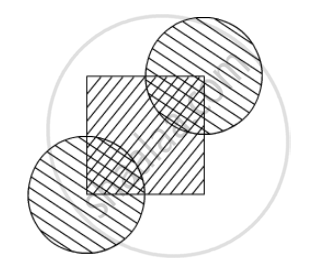
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Diameter of a circular garden is 9.8 m. Find its area.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
Area of the circle obtained in 196 m2 is ______.
