Advertisements
Advertisements
Question
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
Solution
Area of the circle = Area of first circle + Area of second circle
⇒ πR2 = π(r1)2 + π (r1)2
⇒ πR2 = π(24)2 + π(7)2
⇒ πR2 = 576π + 49π
⇒ πR2 = 625π
⇒ R2 = 625
⇒ R = 25
Thus, diameter of the circle = 2R = 50 cm.
APPEARS IN
RELATED QUESTIONS
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
The circumference of a circle is 100 m. The side of a square inscribed in the circle is
The area of a circle is 220 cm2. The area of ta square inscribed in it is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
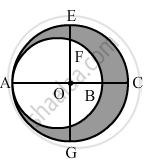
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
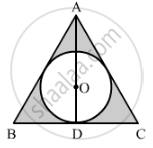
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
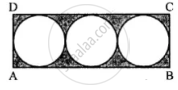
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
