Advertisements
Advertisements
Question
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
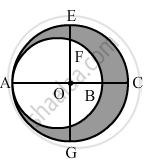
Solution
We have :
OA = OC = 27 cm
AB = AC - BC
= 54 - 10
= 44
AB is the diameter of the smaller circle.
Thus, we have:
Radius of the smaller circle `="AB"/2 = 44/2 = 22 "cm"`
Area of the smaller circle = πr2
`=22/7xx22xx22`
= 1521.14 cm2
Radius of the larger circle `= "AC"/2 = 54/2 = 27 "cm"`
Area of the larger circle = πr2
`= 22/7xx27xx27`
= 2291.14 cm2
∴ Area of the shaded region = Area of the larger circle -- Area of the smaller circle
= 2291.14 - 1521.14
= 770 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
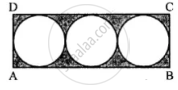
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
