Advertisements
Advertisements
Question
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
Solution

Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm
⇒ `asqrt2 = 8`
⇒ `a = 4sqrt2` cm
Now, Diagonal of a square = Diameter of a circle
⇒ Diameter of circle = 8
⇒ Radius of circle = r = `"Diameter"/2`
⇒ `r = 8/2 = 4` cm
∴ Area of circle = `pir^2 = pi(4)^2`
= `16pi xx cm^2`
and Area of square = `a^2 = (4sqrt2)^2`
= 32 cm2
APPEARS IN
RELATED QUESTIONS
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
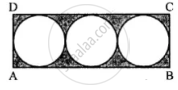
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
Find the area of the dining table whose diameter is 105 cm
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
Area of circle of radius ‘n’ units is
The area of a circle is 154 cm2. Its diameter is ____________.
