Advertisements
Advertisements
Question
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

Solution
In the right angled : ΔACB
`AB^2=BC^2+AC^2`
⇒ `17^2=BC^2+15^2`
⇒ `17^2-15^2=BC ^2`
⇒ `64=BC^2`
⇒`BC=8 cm`
Perimeter=`AB+BC+CD+AD`
=`17+8+12+9`
= `46 cm^`
Area of `ΔABC=1/2(bxxh`)
=`1/2(8xx15)`
=`60 cm^2`
In : ΔADC
`AC^2=AD^2+CD^2`
So, ΔADC is a right- angled triangle at D
Area of `ΔADC=1/2xxbxxh`
=`1/2xx9xx12`
=`54 cm^2`
∴ Area of the quadrilateral =` Area of ΔABC+Area of ΔADC`
=`60+54`
=`114 cm^2`
APPEARS IN
RELATED QUESTIONS
The floor of a rectangular hall is 24 m long and 18 m wide. How many carpets, each of length 2.5 m and breadth 80 cm, will be required to cover the floor of the hall?
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
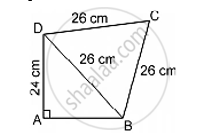
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
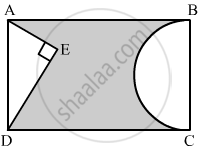
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
