Advertisements
Advertisements
Question
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
Solution
Diameter = 56 cm
∴ Radius, r = 28 cm
∴ Distance travelled in 1 revolution
i.e. circumference = `2pir = 2 xx 22/7 xx 28 = 176` cm
∴ Distance travelled in 45 revolution
= `176 xx 45 = 7920 "cm" = 7920/(100 xx 1000)`km
Time = 10 sec = `10/(60 xx 60)` hr.
Speed = `(7920/(100 xx 1000))/(10/(60 xx 60))`m
= `7920/(100 xx 1000) xx (60 xx 60)/10 = 28512/1000` km/hr
= 28.512 km/hr
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
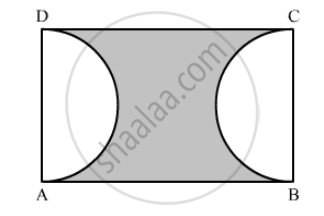
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
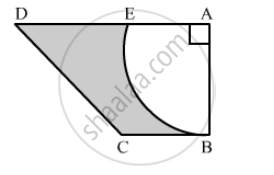
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
If the radius of a circle is diminished by 10%, then its area is diminished by
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
The area of a sector whose perimeter is four times its radius r units, is
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
On increasing the diameter of a circle by 40%, its area will be increased by
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
