Advertisements
Advertisements
Question
The area of a sector whose perimeter is four times its radius r units, is
Options
\[\frac{r^2}{4}\]
2r2 sq. units
r2 sq.units
Solution
We know that perimeter of the sector= `2r+θ/360xx2pir`
We have given that perimeter of the sector is four times the radius.
`2r+θ/360x2pir=4r`
Subtracting 2r from both sides of the equation,
`∴ θ/360xx2pir^=4r-2r`
`∴ θ/360xx2pir=2r`
Dividing both sides of the equation 2r we get,
`θ/360=pi=1`
`∴ θpi/360=1`.............(1)
Let us find the area of the sector.
∴ Area of the sector=`θ/360 pir^2`
Substituting `θpi/360=1` we get,
Area of the sector=`r^2`
Hence, area of the sector is `r^2 `sq.units
APPEARS IN
RELATED QUESTIONS
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

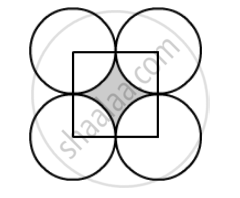
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
The area of a circle is 98.56 cm2. Find its circumference.
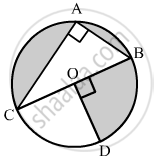
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
If the radius of a circle is doubled, its area becomes ____________.
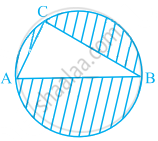
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).