Advertisements
Advertisements
Question
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
Solution
In a right isosceles triangle, base = height = a
Therefore,
`Area of a triangle=1/2xxbasexxheight=1/2xxaxxa=1/2a^2`
Further, given that area of isosceles right triangle=`200cm^2`
⇒`1/2a^2=200`
⇒`a^2=400`
Or,` a=sqrt400=20cm`
In an isosceles right triangle, two sides are equal ( 'a`) and the third side is the hypotenuse,
i.e, 'c'
Therefore, `C=sqrt(a^2+a^2)`
=`sqrt(2a^2)`
=`asqrt2`
=`20xx1.41`
=`28.2 cm`
Perimeter of the triangle=` a+a+c`
=`20+20+28.2`
=`68.2cm`
The length of the hypotenuse is 28.2 cm and the perimeter of the triangle is 68.2 cm.
APPEARS IN
RELATED QUESTIONS
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
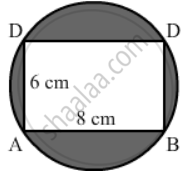
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
