Advertisements
Advertisements
Question
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
Solution
Given:
Base = 80 cm
Area = 360
Area of an isosceles triangle=`(1/4 bsqrt(4a^2-b^2))`
⇒`360=1/4xx80sqrt(4a^a-80^2)`
⇒`360=20sqrt(4a^2-6400)`
⇒`18=2sqrt(a^2-1600)`
⇒`9=sqrt(a^2-1600)`
Squaring both the sides, we get:
⇒`81=a^2-1600`
⇒`a^2=1681`
⇒`a=41cm`
Perimeter=`(2a+b)`
=`[2(41+80)]=82+82=162cm`
So, the perimeter of the triangle is 162 cm.
APPEARS IN
RELATED QUESTIONS
Find the area of the following circles, given that radius = 5 cm.
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
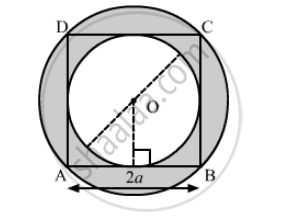
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
The area of a circular path of uniform width h surrounding a circular region of radius r is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
