Advertisements
Advertisements
प्रश्न
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
उत्तर
Given:
Base = 80 cm
Area = 360
Area of an isosceles triangle=`(1/4 bsqrt(4a^2-b^2))`
⇒`360=1/4xx80sqrt(4a^a-80^2)`
⇒`360=20sqrt(4a^2-6400)`
⇒`18=2sqrt(a^2-1600)`
⇒`9=sqrt(a^2-1600)`
Squaring both the sides, we get:
⇒`81=a^2-1600`
⇒`a^2=1681`
⇒`a=41cm`
Perimeter=`(2a+b)`
=`[2(41+80)]=82+82=162cm`
So, the perimeter of the triangle is 162 cm.
APPEARS IN
संबंधित प्रश्न
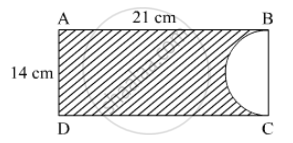
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
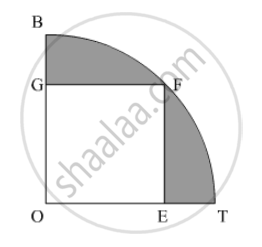
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
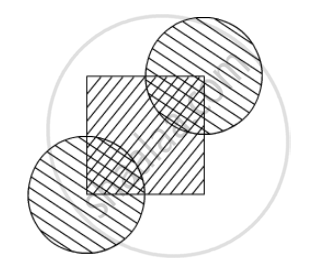
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
The area of the sector of angle θ° of a circle with radius R is
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.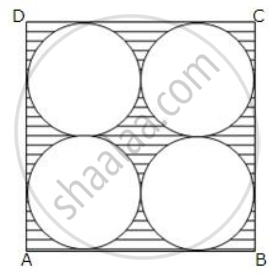
Find the area of the remaining card-board.
The area of the circle whose diameter is 21 cm is ____________.
