Advertisements
Advertisements
प्रश्न
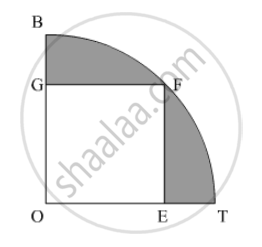
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
उत्तर
We have to find the area of the shaded portion. We have, `OE=20cm`and OEFG is a square.
Use Pythagoras theorem to find OF as,
`OF=(sqrt((20)^2+(20)^2))cm`
`= 20sqrt2 cm`
So, radius of the circle,
`OF=20sqrt2 cm`
Therefore area of the shaded region,
`"Area of the shade region=(Area of quadrant of circle)-(Area of square)"`
So,
Area of the shaded region =`(pi(OF)^2)/4-(OE)^2`
`(22/7)((20sqrt2^2)/4)-(20)^2`
=`628-400`
`=228 cm^2`
APPEARS IN
संबंधित प्रश्न
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
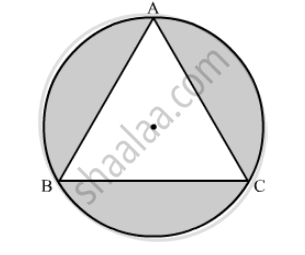
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
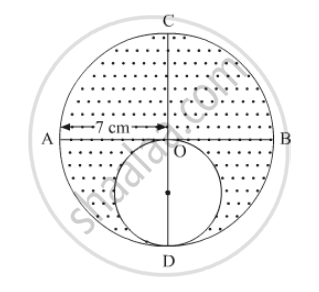
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
In the following figure, the area of the shaded region is
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
