Advertisements
Advertisements
प्रश्न
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
पर्याय
34
26
17
14
उत्तर
Let the diameter of the larger circle be d
Now, Area of larger circle = Area of circle having diameter 10 cm + Area of circle having diameter 24 cm
\[\Rightarrow \pi \left( \frac{d}{2} \right)^2 = \pi \left( \frac{10}{2} \right)^2 + \pi \left( \frac{24}{2} \right)^2 \]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 = \left( 5 \right)^2 + \left( 12 \right)^2\]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 = {13}^2 \]
\[ \Rightarrow \frac{d}{2} = 13\]
\[ \Rightarrow d = 26 cm\]
APPEARS IN
संबंधित प्रश्न
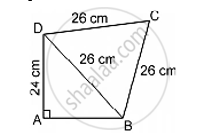
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
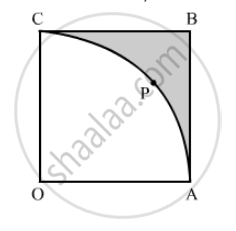
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
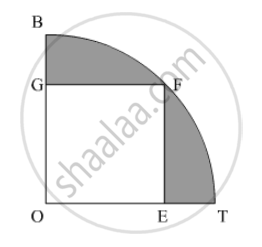
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
