Advertisements
Advertisements
प्रश्न
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
पर्याय
\[2\sqrt{3} - 1 c m^2\]
\[4\sqrt{3} - 1 c m^2\]
\[6\sqrt{3} - 1 c m^2\]
\[8\sqrt{3} - 1 c m^2\]
उत्तर
We have the following diagram.
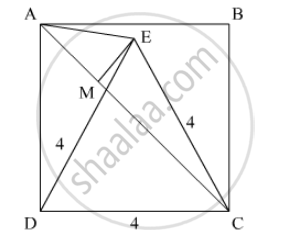
Since `ΔCED` is equilateral,
Therefore,
`EC=CD=DE=4 cm`
Now, `∠ ECD=60°`
Since AC is diagonal of sqr.ABCD
Therefore,
`∠ACD=45°`
Therefore we get,
`∠ECA=∠ECD-∠ACD`
`=60°-45°`
`=15°`
Now, in `ΔACE`, draw a perpendicular EM to the base AC.
So in `Δ EMC`
`sin 15°=(EM)/(EC)`
`=(EM)/4`
Therefore,
`EM=sqrt2(sqrt3-1)`
Now in `ΔAEC`
ar `(ΔAEC=1/2) (AC)(EM)`
`=4(sqrt3-1)cm^2`
APPEARS IN
संबंधित प्रश्न
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
If diameter of a circle is increased by 40%, then its area increase by
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.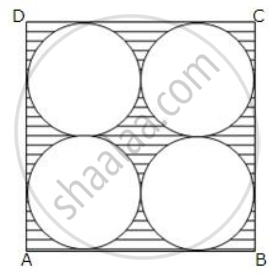
Find the area of the remaining card-board.
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
