Advertisements
Advertisements
प्रश्न
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
पर्याय
12 cm
16 cm
8 cm
10 cm
उत्तर
We have given length of the arc and area of the sector bounded by that arc and we are asked to find the radius of the circle.
We know that area of the sector `θ/360xx2pir`
Now we will substitute the values.
Area of the sector=`θ/360xxpir^2`
`20 pi=θ/360xxpir^2 ............(1)`
Length of the arc=`θ/360xx2pi r`
`5pi=θ/360xx2pir..............(2)`
Now we will divide equation (1) by equation (2),
`(20pi)/(5pi)=(θ/360xxpir^2)/(θ/360xx2pir)`
Now we will cancel the like terms.
`20/5=r^2/(2r)`
`∴ 4=r/2`
`∴=8`
Therefore, radius of the circle is 8 `cm`
APPEARS IN
संबंधित प्रश्न
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
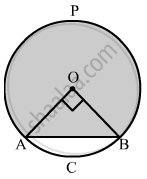
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
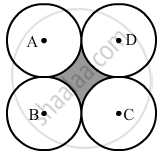
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
