Advertisements
Advertisements
प्रश्न
The area of the circle that can be inscribed in a square of side 10 cm is
पर्याय
40 π cm2
30 π cm2
100 π cm2
25 π cm2
उत्तर
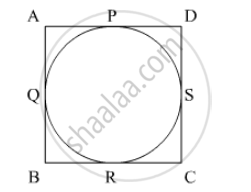
We know that ABCD is a square of length 10 cm. A circle is inscribed in the square therefore, all the sides of the square are become tangents of the circle.
By, the tangent property, we have
`AP=PD=5`
`AQ=QB=5`
`BR=RC=5`
`CS+DS=5`
If we join PR then it will be the diameter of the circle of 10 cm.
Therefore, radius of the circle = 5cm
∴ Area of the circle=`pir^2`
∴ Area of the circle=`pixx5^2`
∴ Area of the circle=`25pi`
Therefore, area of the circle is `25picm^2`
APPEARS IN
संबंधित प्रश्न
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
The circumference of a circular table is 88 m. Find its area.
