Advertisements
Advertisements
Question
The area of the circle that can be inscribed in a square of side 10 cm is
Options
40 π cm2
30 π cm2
100 π cm2
25 π cm2
Solution
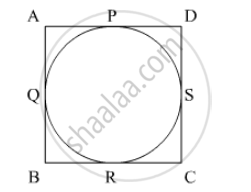
We know that ABCD is a square of length 10 cm. A circle is inscribed in the square therefore, all the sides of the square are become tangents of the circle.
By, the tangent property, we have
`AP=PD=5`
`AQ=QB=5`
`BR=RC=5`
`CS+DS=5`
If we join PR then it will be the diameter of the circle of 10 cm.
Therefore, radius of the circle = 5cm
∴ Area of the circle=`pir^2`
∴ Area of the circle=`pixx5^2`
∴ Area of the circle=`25pi`
Therefore, area of the circle is `25picm^2`
APPEARS IN
RELATED QUESTIONS
A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
In the following figure find the area of the shaded region. (Use π = 3.14)
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
If diameter of a circle is increased by 40%, then its area increase by
The cost of fencing a circular field at the rate of Rs 25 per metre is Rs 5500. The field is to be ploughed at the rate of 50 paise per m2 . Find the cost of ploughing the field. [Take `π =22/7`].
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
