Advertisements
Advertisements
Question
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
Solution
We have the following situation
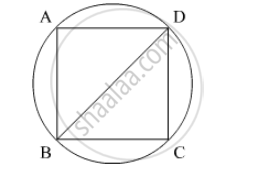
Let BD be the diameter and diagonal of the circle and the square respectively.
We know that area of the circle =`pir^2`
Area of the square = `"side"^2`
As we know that diagonal of the square is the diameter of the square.
Diagonal=`2r`
Side of the square= `"diagonal"/sqrt2............(1)`
Substituting "diagonal"=2r in equation (1) we get,
side of the square=`(2r)/sqrt2`
Now we will find the ratio of the areas of circle and square.
Area of circle/Area of square=`(pir^2)/((2r)/sqrt2)^2`
Now we will simplify the above equation as below,
Area of circle/Area of square=`(pir^2)/(r^2/2)`
Area of circle/Area of square=`pir^2xx2/(4r^2)`
Hence, `"Area of circle"/"Area of square"-pi/2`
Therefore, ratio of areas of circle and square is `pi:2`
APPEARS IN
RELATED QUESTIONS
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
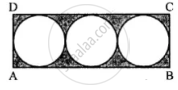
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
